Abstract
Das Ziel dieser Forschungsarbeit ist es, verschiedene Arten von Untergrundtypen mithilfe eines Machine Learning Modells vorhersagen zu können. Verwendet werden dafür beim Fahrradfahren aufgenommene Beschleunigungsdaten, die mit den Sensoren unterschiedlicher Smartphones aufgezeichnet werden. Um die Zielsetzung zu erreichen, werden zunächst Datensätze zum Training des Modells aufgenommen und verarbeitet. In aufeinanderfolgenden Schritten werden Probleme, die mit den Daten und der Zielsetzung einhergehen, angegangen und bestmöglich gelöst. Anschließend werden statistische Feature extrahiert, mit denen ein Machine Learning Modell trainiert wird. Evaluiert wird dieses Modell mit unabhängig entstandenen Testdaten, die nicht im Training verwendet werden. Dabei wird deutlich, dass die Modelle auf den Trainingsdaten gute Genauigkeiten erreichen können, jedoch auf den Testdaten weniger genaue Vorhersagen treffen. Daran wird deutlich, dass einige der gewählten Untergrundtypen vom Machine Learning Modell nicht exakt voneinander getrennt werden können. Basierend darauf ist es vorstellbar, die Vorhersage auf Basis von Klassen durch eine Regression zu ersetzen und Untergründen einen Score für die Befahrbarkeit zuzuweisen.
Analyse von Bodenbeschaffenheiten beim Fahrradfahren
Niclas Bruhns, Nils-Hendrik Meier, Lennart Popkes
Github Repository: https://github.com/NilsHMeier/LG04QS_Cycling
Datenerhebung
Für das Sammeln von Daten wurden drei unterschiedliche Smartphones mit der App „phyphox“ ausgestattet. Diese ermöglicht die Aufnahme von Sensordaten mit dem Smartphone, in unserem Fall die Aufnahme von Beschleunigungsdaten. Alle Smartphones wurden während der Datenaufnahme senkrecht mit dem Bildschirm nach außen in der Hosenseitentasche positioniert. Insgesamt wurden 70 Messungen über einen Zeitraum von drei Wochen durchgeführt, die zusammengerechnet eine Messzeit von zwei Stunden ergeben. Gemessen und aufgenommen wurden Beschleunigungsdaten als CSV Dateien von den folgenden Untergrundtypen:
Asphalt, Radweg, Waldweg, Schotter und Kopfsteinpflaster.
Datenverarbeitung
In diesem Schritt werden die Beschleunigungsdaten jeweils am Anfang und am Ende der Messung geschnitten, um so das anfängliche Anfahren und das abschließende Abbremsen des Fahrrades aus den Messdaten zu entfernen. Es wird also ein Offset von den Daten abgezogen, um irrelevante Daten zu löschen. In unserem Projekt werden die Trainingsdaten für das Machine Learning mit manuellen Offsets verarbeitet, um eine optimale Trainingsgrundlage zu schaffen. Im Anschluss daran geschieht das Testen des Modells mit einem vordefinierten Offset von zehn Sekunden.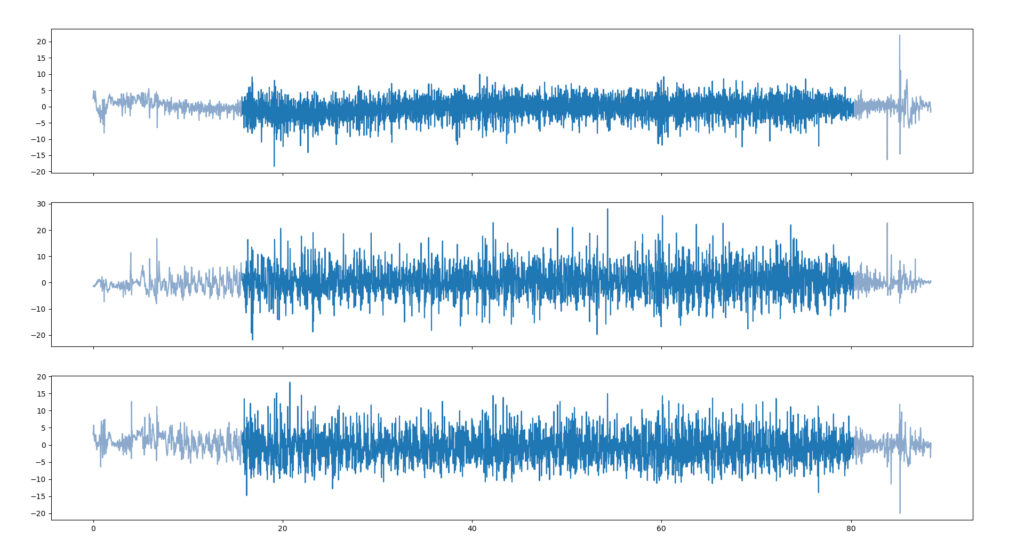
Im nächsten Schritt der Datenverarbeitung wird die Herausforderung der verschiedenen Fahrräder und damit verbundenen Federungen gelöst. Zunächst wurde diese Problematik vernachlässigt, wodurch jedoch die Schritte des Feature Engineerings und des Machine Learnings nicht die erwünschten Ergebnisse brachten. In der Analyse von zwei Asphalt Samples, die zeitgleich auf der gleichen Strecke mit verschiedenen
Fahrrädern aufgenommen wurden, fielen deutliche Unterschiede in den gemessenen Beschleunigungen auf. Das lässt sich mit den unterschiedlichen Federungen der beiden Fahrräder erklären. Federungssysteme sind darauf ausgelegt, Energie der Umwelt (z.B. Unebenheiten) aufzunehmen und damit die Fahrt angenehmer zu machen. Wenn ein Fahrrad mehr gefedert ist, wird mehr Energie aufgenommen. Damit zusammenhängend wirkt eine geringere Kraft auf den Fahrer und der Beschleunigungssensor in der Hosentasche nimmt geringere Beschleunigungen auf. Um dieses Problem zu lösen und die Daten vergleichbar zu machen, wird der Federungskoeffizient (engl. suspension coefficient, kurz SPC) eingeführt. Dabei werden Daten vom ungefederten Fahrrad als Referenz angenommen und Messungen von gefederten Fahrrädern werden über den Koeffizienten auf ein ähnliches Niveau angehoben. Der Koeffizient wird nicht direkt als Faktor, sondern in der Form processed_data = raw_data / (1 - coefficient) auf die Daten angewandt. Das heißt bei einem Koeffizienten von null bleiben die Daten unverändert. Die Abbildung zeigt den tatsächlichen Faktor, der einem Koeffizienten entspricht.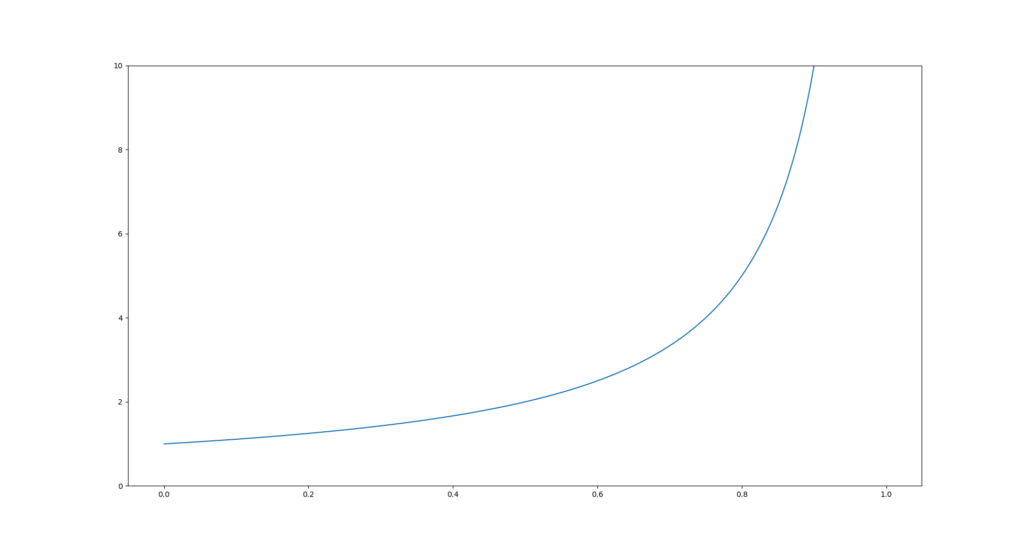
Durch die Aufnahme der Daten mit dem Smartphone in der Hosentasche ist die Tretbewegung beim Fahren deutlich in den Daten zu erkennen.
Unterschiedliche Fahrer treten mit verschiedenen Frequenzen und auch während der Fahrt kann diese z. B. durch Schaltvorgänge stark schwanken. Die Tretbewegung liegt in einem Frequenzbereich von 0 bis 2 Hz bzw. 0 bis 120 U/min. Des weiteren soll das Grundrauschen des Sensors aus dem Signal entfernt werden, da dies ungewollte Effekte bei der Verarbeitung durch Machine Learning Modelle haben könnte. Die verwendeten Beschleunigungssensoren arbeiten mit einer Frequenz von 100 Hz bzw. 200 Hz. Da die Obergrenze unterhalb der halben Abtastfrequenz liegen muss, um überhaupt eine Auswirkung zu haben, haben wir uns für eine Obergrenze von 30 Hz entschieden, denn bei einer Abtastfrequenz von 100 Hz kann die höchste gemessene Frequenz max. 50 Hz betragen. Jedoch sollte sie auch nicht zu niedrig gewählt werden, da sonst Details der Messung verloren gehen, die eine Aussage über den befahrenen Untergrund geben könnten. Um die nicht gewünschten Frequenzbänder aus dem Signal zu entfernen, wird ein Bandpass-Filter verwendet. Die Abbildung zeigt die Daten vor und nach dem Filter.
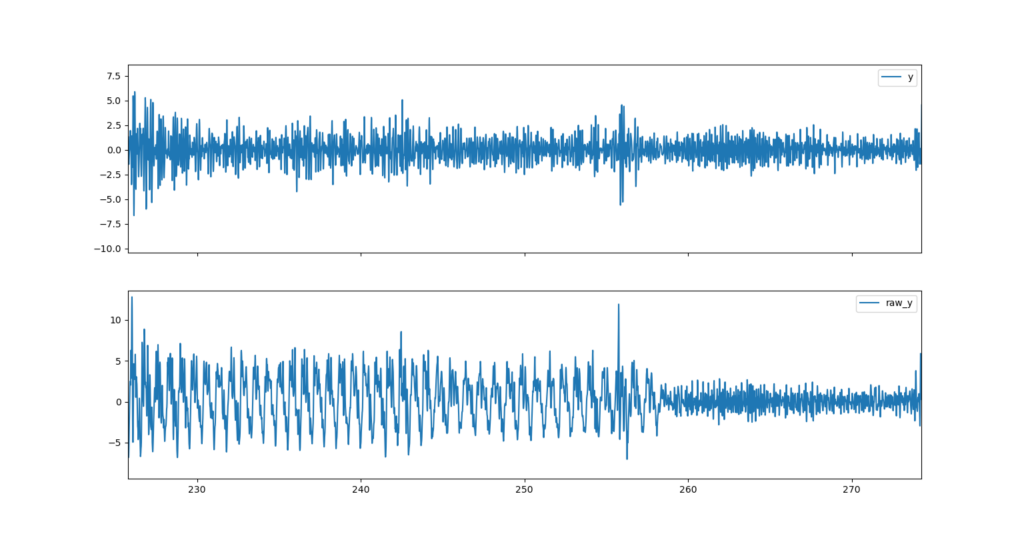
Während der Aufnahme von Beschleunigungsdaten werden nicht nur für das Machine Learning relevante Untergrunddaten erfasst, sondern auch unerwünschte Ausreißer, die z.B. durch Schlaglöcher im Asphalt oder Stöcke auf einem Fahrradweg entstehen. Diese gilt es aus den Datensätzen zu entfernen, da sie die weitere Verarbeitung verfälschen. Als Ausreißer werden allgemein Datenpunkte bezeichnet, die sich vom Großteil der restlichen Daten unterscheiden und Werte weit entfernt des Durchschnitts annehmen. Mithilfe einer Outlier Detection (zu Deutsch: Ausreißererkennung) werden eben diese Datenpunkte erkannt und können anschließend entfernt werden. Für unsere Datenverarbeitung haben wir uns für eine verteilungsbasierte Outlier Detection entschieden. Dabei wird angenommen, dass Daten einer Messung um den Mittelwert herum normalverteilt sind. Daraus ergibt sich für Datenpunkte eine Wahrscheinlichkeit, dass sie zu dieser Normalverteilung gehören. Über das
Chauvenet-Kriterium kann eine Grenze festgelegt werden, ab der Datenpunkte als Ausreißer behandelt werden. Je nachdem, wie hoch das Kriterium angesetzt wird, ändert sich die Anzahl der erkannten Ausreißer. Die Abbildung visualisiert diesen Zusammenhang.
Feature Engineering
Nachdem das Preprocessing abgeschlossen ist, können aus den verarbeiteten Daten Feature generiert werden, auf denen später die Machine Learning Modelle trainiert werden. Pro Beschleunigungsachse wurden vier Feature ausgewählt, wodurch sich bei drei Achsen folglich eine Gesamtzahl von 12 Feature ergibt. Diese sind der Durchschnitt, die Standardabweichung sowie Minimum und Maximum. Die Feature beschränken sich auf statistische Kenngrößen, da diese in der Visualisierung bereits deutliche Unterschiede aufgezeigt haben. Zur beispielhaften Visualisierung der gewählten Feature ist in der Abbildung die Standardabweichung der Beschleunigungsdaten von allen Messungen als dreidimensionaler Scatter Plot dargestellt. Bereits hier ist eine Trennung der Untergrundtypen ersichtlich. Deutlich zu erkennen ist die im Vergleich hohe Standardabweichung der Beschleunigungsdaten von Kopfsteinpflaster (türkis) und zum Teil von Schotter (gelb). Ebenso Asphalt (rot) lässt sich aufgrund einer geringen Standardabweichung aus dem Graphen erkennen. Schwierigkeiten stellen hier die Untergrundtypen Radweg, Waldweg und zu einem gewissen Anteil auch Schotter dar, da diese in vielen Fällen ähnliche Standardabweichungen vorweisen. Aus diesem Grund wurden daraufhin die weiteren Feature Minimum, Maximum und der Durchschnitt mit einbezogen, um die Güte des Modells zu stärken.
Machine Learning
Die verwendeten Machine Learning Algorithmen, auf die später kurz eingegangen wird, fallen unter das sogenannte „Überwachte Lernen“ (engl. Supervised Learning). Diese Variante des maschinellen Lernens basiert darauf, dass die „Ground Truth“ über verwendete Daten bekannt ist. Die Daten, die im Training des Modells verwendet werden, sind gelabelt und damit eindeutig klassifiziert bzw. zugeordnet. Auf dieser Basis kann ein Algorithmus Regelmäßigkeiten erkennen und Regeln ableiten, nach denen die Daten geordnet sein könnten. Als Klassifikationsmodelle wurden die „Support Vector Machine“ (kurz SVM) sowie „k-Nearest-Neighbours“ (kurz KNN) verwendet, um verschiedene Aspekte des Lernprozesses verdeutlichen zu können. Die Funktionsweise von KNN basiert darauf, die Klasse bzw. das Label von den k nächsten Nachbarn bzw. Datenpunkten zu ermitteln und den vorherzusagenden Datenpunkt nach dem Mehrheitsprinzip zuzuweisen. Im Falle, dass für zwei oder mehr Klassen gleich viele Nachbarn vorhanden sind, wird nach dem Zufallsprinzip entschieden. Die SVM dagegen trennt die Trainingsdaten und teilt sie in Bereiche auf. Je nach Form der Daten und Einstellungen der SVM werden die Daten so transformiert, dass sie getrennt werden können. Beispielsweise bilden im zweidimensionalen Raum Linien bzw. Vektoren und im dreidimensionalen Raum Ebenen die Abgrenzung(en) zwischen einzelnen Klassen. Über den sogenannten Kernel kann festgelegt werden, in welcher Form die Daten getrennt werden sollen (u.a. linear oder poly).
Die Daten werden in drei Datensätze unterteilt, namentlich Trainings-, Validation- und Testdaten. Das Modell wird auf Basis der Trainingsdaten trainiert und abschließend mit den Testdaten überprüft. In einem Zwischenschritt wird die Güte des Trainings durch die Validationdaten überprüft. Die folgende Abbildung verdeutlicht die Unterteilung der Daten.
Die Optimierung in Bezug auf die verschiedenen Phasen erfolgt durch die Variation der modellspezifischen Hyperparameter. Unter diesem Begriff versteht man Parameter, die vor dem Durchlaufen des eigentlichen Trainings festgelegt werden müssen und den dahinter liegenden Algorithmus beeinflussen. Falls der Anwender keine Parameter festlegt, werden die Standardparameter verwendet. Je nach Problemstellung sind diese jedoch nicht optimal und das Modell erzielt keine guten Ergebnisse. Daher können die Parameter über verschiedene Verfahren optimiert werden.
Bei KNN wird lediglich die Anzahl der Nachbarn variiert, die für die Klassifizierung des Datenpunktes abgefragt werden. Im Falle der SVM sind das die Parameter „C“ und „Gamma“. Wie bereits erläutert, basiert die Funktionsweise der SVM auf der Trennung von Datenpunkten. Standardmäßig wird im Training versucht, die Daten so zu trennen, dass alle Datenpunkte der richtigen Klasse zugeordnet sind. Über den Parameter C wird für falsch klassifizierte Punkte eine „Strafe“ eingeführt, über die die Genauigkeit der Grenzen verändert werden kann. Bei einem kleinen C ist die Strafe gering und die Grenzen werden daher eher weich gezogen. Der zweite variierte Hyperparameter Gamma legt fest, wie eng die Grenzen um ähnliche Datenpunkte gelegt werden sollen. Im Falle eines kleines Gammas werden auch weiter entfernte Datenpunkte noch der Klasse zugeordnet. Umgekehrt werden die Grenzen bei einem großen Gamma sehr eng um die Trainings-Datenpunkte gesetzt, was zu sehr spezifischen Klassenbereichen und damit zum „Overfitting“ führen kann. Das Modell erreicht dann in der Trainingsphase sehr hohe Scores, hat jedoch mit der Vorhersage von neuen Daten in der Testphase große Schwierigkeiten.
Die untenstehende Abbildung zeigt den Trainingsverlauf vom KNN Modell unter Variation der Anzahl der verwendeten Nachbarn k. In Abhängigkeit des Hyperparamters verändern sich die Scores der Trainings- und Testphase. Während der Trainingsscore beständig abnimmt, erreicht der Testscore bei knapp 40 Nachbarn den höchsten Wert.
Wie bereits genannt, werden die etwa 70 Datensätze in zwei Kategorien geteilt: Trainingsdaten (70%) und Validation-Daten (30%). Mit den Trainingsdaten wird das Modell trainiert und anschließend mit den Validation-Daten getestet. Da die Trainingsdaten und Validation-Daten zufällig geteilt werden, sind sie relativ ähnlich zueinander. Aus der untenstehenden Confusion Matrix ist zu erkennen, dass die meisten Validation-Datensätze korrekt klassifiziert werden. Nach der Optimierung der SVM auf die Validation-Daten konnten wir einen maximalen Score von 92.5% erreichen.
Wie im Learning Setup genannt, wird mit dem Testdatensatz die Performance des Modells bei unbekannten Daten getestet. Daraus können folgende Schlüsse gezogen werden:
- Die Untergrundtypen „Asphalt“ und „Kopfsteinpflaster“ werden sehr gut vorhergesagt. Dies sind die eindeutigen Untergrundtypen und daher leicht von den anderen zu unterscheiden.
- „Radweg“ und „Schotter“ werden häufig fälschlicherweise als Asphalt klassifiziert. Vermutlich liegt dies daran, dass in den Trainingsdaten auch Asphalt-Sample da bei sind, bei denen die befahrene Straße uneben war oder viele Schlaglöcher enthielt. Einige Schotter- und Radwege sind sehr glatt und können daher leicht mit Asphalt verwechselt werden.
- Die drei Untergrundtypen „Radweg“, „Schotter“ und „Waldweg“ werden häufig vom Modell verwechselt. Problematisch ist bei diesen drei Typen, dass sie zum Teil nicht eindeutig zu unterscheiden sind und die Labels daher nicht eindeutig gesetzt sind. Es gibt viele Wege, die Elemente eines Schotterweges, aber auch Elemente eines Waldweges haben, und dort ist eine klare Zuordnung des Labels schwierig.
