Distanzmetriken

Inhalt

Distanzmetriken oder auch Distanzmaße werden verwendet, um die Ähnlichkeit von Daten(-punkten) zu bestimmen und einen Vergleich zu ermöglichen. Statt Ähnlichkeit von Daten spricht man dabei auch häufig vom Abstand. Distanzmaße bilden die basis für alle distanzbasierten Verfahren, wie etwa K-Nearest-Neighbour als Klassifikationsverfahren oder auch SMOTE (Syntetic Minority Class Oversampling Technique) aus dem Bereich des Sampling. Die Auswahl des Distanzmaßes spielt jeweils eine wichtige Rolle und wird im letzten Teil dieses Beitrags kurz näher erläutert.

Wichtige Distanzmaße #

Nachfolgend werden vier wichtige verschiedene Distanzmaße vorgestellt:

Das wohl bekannteste Distanzmaß ist die Euklidische Distanz, die zur Berechnung des Abstands von Punkten im n-dimensionalen Raum genutzt werden kann. Sie ist die direkte Verbindung zwischen zwei Punkten und durch die folgende Formel gegeben:
Ein weiteres Distanzmaß ist die Manhattan Distanz, die sich an der Struktur der Häuserblöcke und Straßen in New York orientiert. Sie setzt sich zusammen aus der Summe aller absoluten Differenzen und ist durch die folgende Formel gegeben:
Die allgemeine Form der Euklidischen Distanz ist die Minkowski Distanz mit dem Parameter p. F ̈ur p=1 ergibt sich die Manhattan Distanz, f ̈ur p=2 die Euklidische Distanz. Die allgemeine Formel hat die folgende Form:
Die Cosinus ̈Ahnlichkeit ist eine Distanzmetrik, die häufig im Kontext der Textverarbeitung eingesetzt wird. Sie nimmt Werte zwischen 0 und 1 an, die jedoch immer relativ zueinander betrachtet werden müssen. Die Berechnung erfolgt über die Cosinus Ähnlichkeit wie folgt:

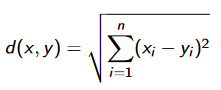
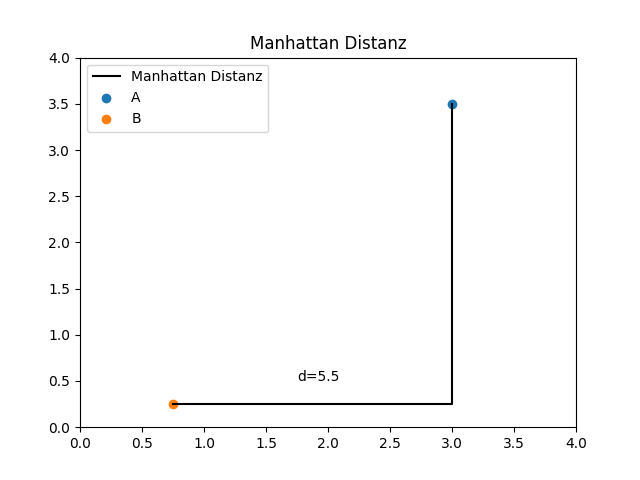
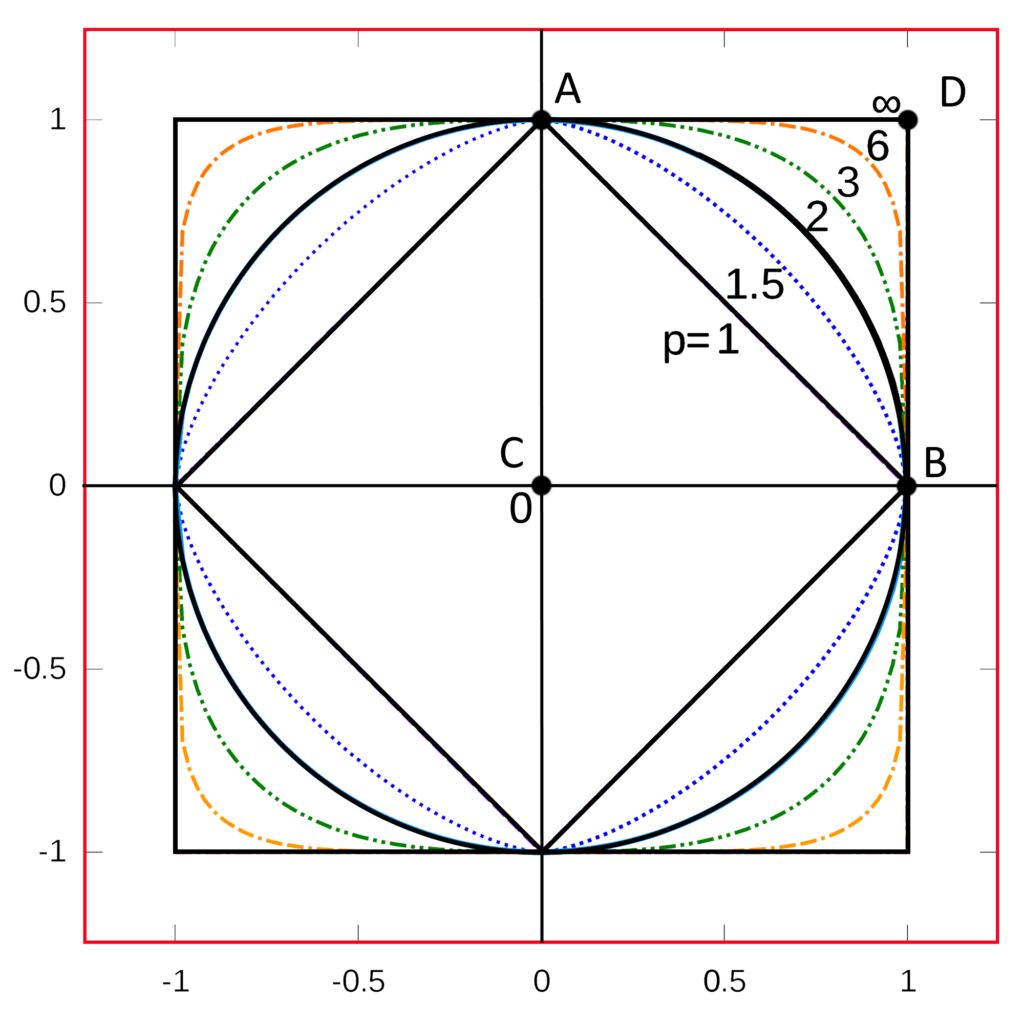
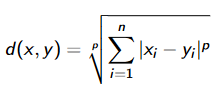
Auswahl der richtigen Distanzmetrik #

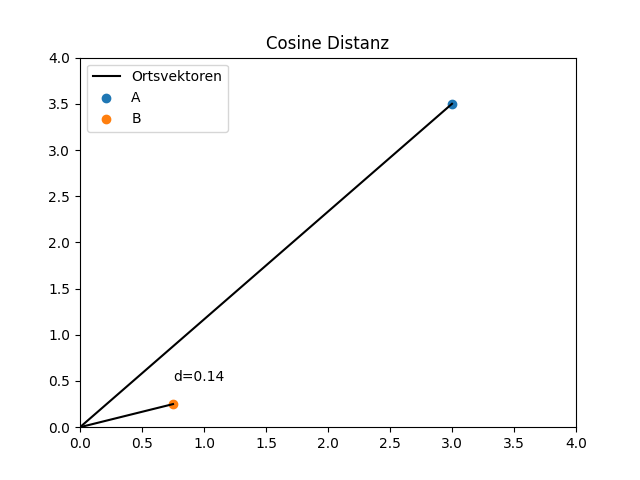
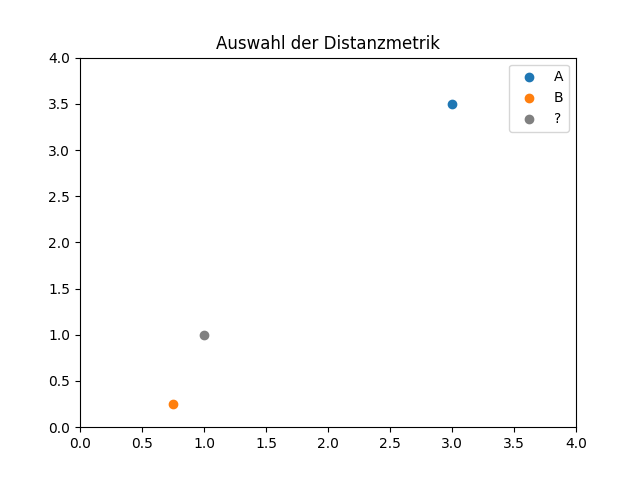
Die Auswahl der Distanzmetrik spielt eine wichtige Rolle, da sie maßgeblich die Ergebnisse von distanzbasierten Verfahren beeinflusst. Im Beispiel ermittelt werden, ob Punkt A oder B ähnlicher sind zum neuen grauen Punkt. Bei Auswahl von Manhattan oder Euklidischer Distanz word B als ähnlicher eingestuft, bei Auswahl der Cosine-Distanz jedoch Punkt A.

Daher sollte immer überprüft werden, ob eine bestimmte Distanzmetrik für die Problemstellung geeignet ist und ob die Ergebnisse mit den Erwartungen übereinstimmen.

Bestimmung der Ähnlichkeit zwischen bestehenden Datenpunkten und einem neuen Punkt.

Weiterführende Links #

17 Types of Similarity and Dissimilarity Measures: https://towardsdatascience.com/17-types-of-similarity-and-dissimilarity-measures-used-in-data-science-3eb914d2681
How to decide the perfect distance metric: https://towardsdatascience.com/how-to-decide-the-perfect-distance-metric-for-your-machine-learning-model-2fa6e5810f11

What are your Feelings

Schreibe einen Kommentar